ASMAS SS2024 - Solution 1

Problem 1: Data Collection and First Inspection

Measure width of your left hand in mm and your height in cm and enter that data into a table. From that table create a simple plot using the function plot(). As a demo, we are first running that with random numbers. After that run the same with the collected data

set.seed(1902)
n_nr_obs <- 15
vec_width_random <- rnorm(n_nr_obs, mean = 73, sd = 2.5)
vec_height_random <- rnorm(n_nr_obs, mean = 175, sd = 7.9)
plot(vec_width_random, vec_height_random)

Do the same with the collected data

Order both variables (width and height) in the data according to the width of the left hand, then repeat the plot

vec_order_random <- order(vec_width_random)
vec_ord_width_random <- vec_width_random[vec_order_random]
vec_ord_height_random <- vec_height_random[vec_order_random]
plot(vec_ord_width_random, vec_ord_height_random)

Do the ordered version of the plot

Problem 2: Line Fitting

• Based on the plotted points above what would be a good description of the relationship of width and height?
• How well would a straight line describe the relationship?
• Why do we want to use a straight line?
• What is the meaning of a linear relationship?
• Try to fit different straight lines throught the plotted points by trial and error.

Fitting different lines through the demo

• Try to make statements about how well a given straight line fits the points.

plot(vec_width_random, vec_height_random)
abline(180, 0, col="blue")
abline(170, 0.1, col = "green")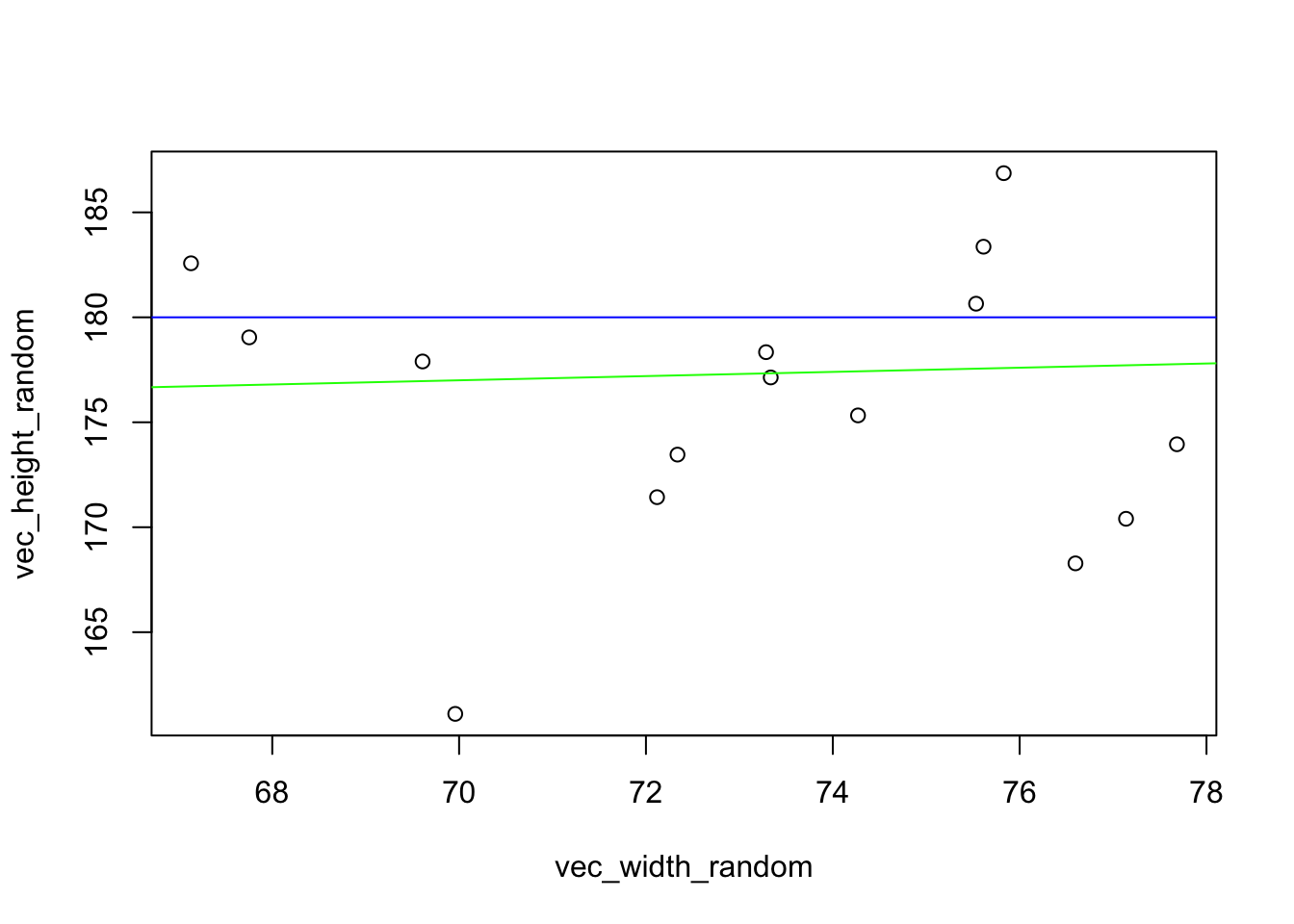

Try to fit some plots for the collected data

• Do some computations related to how well the lines fit the data

Start with blue line

Green line

Additional Problem: Fit a Series of Lines

The following code chunk fits a series of lines and finds the minimum sum of squared residuals